Congetture approvate nelle vite che non tornano
SCIENZA Un percorso attraverso la complessa biografia di alcuni matematici del Novecento. Da Michael Atiyah e i suoi «numeri primi», passando per Schinichi Mochizuki, Peter Scholze e Jakob Stix. E all’affascinante storia del russo Grigorij Perel’man, Masha Gessen ha dedicato di recente un volume
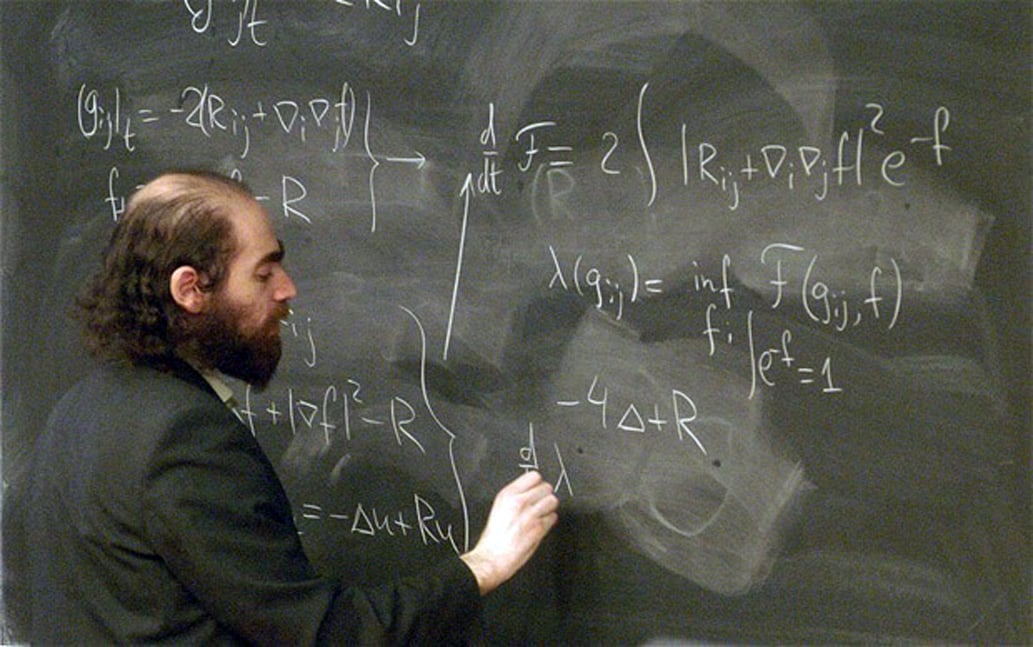 Il matematico russo Grigorij Perel’man che nel 2002 ha dimostrato la validità della congettura di Poincar
Il matematico russo Grigorij Perel’man che nel 2002 ha dimostrato la validità della congettura di PoincarSCIENZA Un percorso attraverso la complessa biografia di alcuni matematici del Novecento. Da Michael Atiyah e i suoi «numeri primi», passando per Schinichi Mochizuki, Peter Scholze e Jakob Stix. E all’affascinante storia del russo Grigorij Perel’man, Masha Gessen ha dedicato di recente un volume
Tra tutte le scienze, la matematica sembra quella più astratta. Per il suo carattere apparentemente assoluto, molti filosofi si sono chiesti se addirittura essa esista indipendentemente dalla mente umana. Cioè se 2+2 facesse 4 ancor prima che Homo sapiens comparisse sulla Terra. Ci sono buoni argomenti a favore e contro questa tesi. Se da ciascuno di due alberi cadono due mele, è indubbio che a terra ci siano quattro mele anche se non ci sono umani in grado di contarle. D’altronde, la matematica è un sistema basato su assiomi che possono essere modificati, come le regole di un gioco di società che finisce quando si chiude la scatola.
SE SI PASSA dalla matematica ai matematici in carne e ossa, l’influenza del fattore umano sui progressi della matematica invece è innegabile. La matematica è una scienza «povera», bisognosa di limitate infrastrutture, dunque il contributo dei singoli ricercatori ha un ruolo predominante. La cronaca scientifica continua a fornire esempi di scoperte matematiche di primissimo livello il cui destino è indissolubilmente legato alle vicende personali dei loro autori. L’ultimo esempio riguarda il matematico britannico Sir Michael Atiyah, che all’età di 89 anni ha annunciato di aver dimostrato la famosa «ipotesi di Riemann». L’ipotesi riguarda le soluzioni di un’equazione formulata dal tedesco Bernhard Riemann nel 1859, correlate a loro volta alla distribuzione dei numeri primi. L’equazione permette di calcolare quanti numeri primi ci sono entro un certo valore ma la sua soluzione si basa su questa ipotesi finora mai dimostrata. L’ipotesi di Riemann permetterebbe di avere una formula per trovare numeri primi molto grandi e la questione avrebbe conseguenze concrete per tutti noi: la difficoltà di trovare numeri primi grandi è alla base di tutti i sistemi crittografici che si utilizzano oggi, dalle telecomunicazioni alle carte di credito e ai bitcoin.
MICHAEL ATIYAH è un mostro sacro della matematica del Novecento, eppure la sua dimostrazione è stata accolta con scetticismo e qualche imbarazzo, e difficilmente verrà pubblicata da qualche rivista specializzata, ciò che le conferirebbe lo statuto di «scoperta». Negli ultimi anni, l’ormai pensionato Atiyah è incorso diverse volte in errori matematici e sarà difficile trovare colleghi disposti a scervellarsi sulla sua presunta dimostrazione. In ballo, tra l’altro, c’è un milione di dollari di premio, perché l’ipotesi di Riemann è uno dei sette «problemi del millennio» su cui il Clay Mathematics Institute di Boston ha messo una taglia. Mai dire mai, perché nulla impedisce che uno scienziato di 89 anni faccia una scoperta eccezionale.
Se la stima di cui gode un matematico non basta a rendere corretta qualunque dimostrazione, è possibile che avvenga il contrario. Cioè, la difficile relazione tra un matematico e la sua comunità può impedire che una grande scoperta venga riconosciuta come tale. Lo dimostra il caso del giapponese Schinichi Mochizuki, un altro gigante della matematica ma all’apice della carriera. Il suo risultato più discusso riguarda la cosiddetta «congettura abc», a proposito di tre numeri qualsiasi legati tra loro dalla semplice relazione a+b=c. Secondo la «congettura abc», il prodotto dei numeri primi che scompongono a, b e c è sempre più piccolo di c tranne in un numero finito di eccezioni. Nonostante le apparenze, questa congettura è ricca di conseguenze in branche fondamentali della matematica. Nel 2012, Mochizuki avrebbe dimostrato la sua validità, ma la dimostrazione è contenuta in una serie di difficilissimi articoli, per un totale di 500 pagine. A causa dell’approccio originale e di un linguaggio matematico impenetrabile, solo pochissimi hanno provato ad analizzarla in dettaglio. Senza la «revisione dei pari» (peer review, in inglese) gli articoli non possono essere pubblicati su una rivista specializzata. Mochizuki avrebbe tutto l’interesse, dunque, a rendere più comprensibile la sua teoria da parte dei colleghi. Invece, il matematico giapponese ha evitato le numerose conferenze dedicate alle sue ricerche. Anzi, non si allontana quasi mai da Kyoto. Finora, solo una dozzina di matematici hanno sostenuto la validità della dimostrazione, ma si tratta soprattutto di colleghi che direttamente o indirettamente collaborano con lui.
LE COSE potrebbero essere cambiate negli ultimi giorni. Come racconta la rivista «Quanta Magazine», i tedeschi Peter Scholze (uno dei migliori matematici del mondo a soli 31 anni e recente vincitore della Medaglia Fields) e Jakob Stix hanno trovato un errore nella dimostrazione della congettura di Mochizuki. Nello scorso marzo, i due si sono recati a Kyoto per parlarne direttamente con lui ma la discussione ha avuto solo il risultato di approfondire la distanza tra le rispettive posizioni. Nel frattempo, la rivista matematica dell’istituto in cui lavora Mochizuki ha comunicato l’intenzione di pubblicare la sua dimostrazione provocando una situazione incresciosa: «quello che a Kyoto è un teorema, nel resto del mondo è ancora una congettura» ha scritto il matematico statunitense Frank Calegari. Finora, ogni richiesta a Mochizuki di scrivere una versione più comprensibile della dimostrazione è caduta nel vuoto.
Talvolta, al contrario, la bontà di una soluzione prevale su qualunque idiosincrasia del suo autore. È la sintesi della vicenda misteriosa del matematico russo Grigorij Perel’man. Su di lui, la giornalista del New Yorker Masha Gessen ha scritto un libro Perfect rigor, appena pubblicato per Carbonio Editore nella traduzione di Olimpia Ellero (pp. 250, euro 17.50). Perel’man nel 2002 ha dimostrato la validità della congettura di Poincaré, altro problema del millennio per il Clay Institute. Secondo la congettura, formulata dal matematico francese nel 1904, ogni varietà tridimensionale semplicemente connessa (cioè priva di «buchi», a differenza per esempio di una ciambella) una può essere deformata fino a trasformarsi in una sfera.
Invece di inviare la sua dimostrazione a una rivista e sottoporsi alla peer review, Perel’man si è limitato a pubblicarla online sull’archivio www.arxiv.org. L’archivio è usato da fisici e matematici per far circolare rapidamente le proprie ricerche, senza aspettare i tempi della pubblicazione sulle riviste scientifiche tradizionali che talvolta richiedono anni di attesa. L’anticonformismo di Perel’man però non si limita all’editoria.
IL MATEMATICO RUSSO, classe 1966, è uno degli ultimi enfant prodige della gloriosa scuola matematica sovietica – vinse le Olimpiadi internazionali di matematica nel 1982. Sia prima che dopo la dimostrazione della congettura di Poincaré, è stato corteggiato dalle migliori università del mondo. Eppure, tranne per brevi periodi, la sua carriera si è svolta tutta all’Istituto Steklov di San Pietroburgo, dove vive in una casa popolare di periferia con la madre. Nel 2005, all’apice del successo, si è licenziato anche dallo Steklov senza lasciare tracce e senza dare spiegazioni. Ha ricevuto i maggiori riconoscimenti internazionali per un matematico, dalla medaglia Fields al milione di euro del Clay Institute, ma li ha regolarmente rifiutati.
I pochissimi che hanno potuto parlarci raccontano di un uomo indisponibile a qualunque compromesso, per il quale persino l’austera comunità scientifica dei matematici risulta contaminata: impensabile sottoporsi ai colloqui di lavoro e premiazioni, o sopportare la competizione con rivali spregiudicati, per uno capace di restituire al suo istituto un bonus di 8mila rubli ritenuto non meritato. Secondo Masha Gessen, che ha scritto un libro su di lui senza riuscire a incontrarlo, la personalità di Perel’man presenta i tipici tratti della sindrome di Asperger come molti altri geniacci, da Albert Einstein a Sheldon Cooper. Nonostante i silenzi, le sfuriate, i tentativi di plagio, la sua dimostrazione è stata infine riconosciuta valida anche dai suoi rivali. Perel’man può finalmente ignorare i premi, le cattedre e la stessa matematica: le sue idee non hanno più bisogno di lui.
I consigli di mema
Gli articoli dall'Archivio per approfondire questo argomento